Depth Post-Processing for Intel® RealSense™ Depth Camera D400 Series
Authors: Anders Grunnet-Jepsen, Dave Tong.
Revision 1.0.2
This article is also available in PDF format.
Introduction
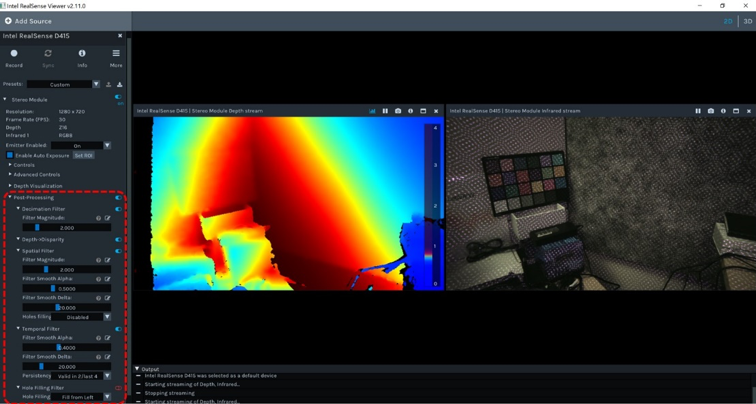
The Intel® RealSense™ D4xx depth cameras can stream live depth (i.e. ranging data) and color data at up to 90 frames per second, and all the processing to generate the depth data is done on-board by the embedded D4 ASIC. This should essentially leave nearly zero burden on the host processor which can then focus instead on the use of the depth data for the application at hand. Although over 40 parameters can be adjusted that affect the calculation of the depth, it should be noted that the ASIC does not perform any post-processing to clean up the depth, as this is left to higher level applications if it is required. In this paper, we discuss some simple post-processing steps that can be taken on the host computer to improve the depth output for different applications, and we look at the trade-offs to host compute and latency. We have included open source sample code in the Intel RealSense SDK 2.0 (libRealSense) that can be used, but it is important to note that many different types of post-processing algorithms exist, and the ones presented here are just meant to serve as an introductory foundation. The librealsense post-processing functions have also all been included into the Intel RealSense Viewer app (shown below), so that the app can be used as a quick testing grounds to determine whether the Intel post-processing improvements are worth exploring.
Simple Post-Processing
As mentioned in a different white paper, to get the best raw depth performance out of the Intel RealSense D4xx cameras, we generally recommend that the Intel RealSense D415 be run at 1280x720 resolution, and the Intel RealSense D435 to be run at 848x480 resolution (with only a few exceptions). However, while many higher level applications definitely need the depth accuracy and low depth noise benefits of running at the optimal high resolution, for most use cases they actually do not need this many depth points, i.e. high x & y resolution. In fact, the applications may have their speed and performance negatively impacted by having to process this much data. For this reason our first recommendation is to consider sub-sampling the input right after it has been received:
- Sub-sampling: While sub-sampling can be done by simply decimating the depth map by taking for example every nth pixel, we highly recommend doing slightly more intelligent sub-sampling of the input depth map. We usually suggest using a “non-zero median” or a “non-zero mean” for a pixel and its nearby neighbors. Considering the computation burden, we suggest using “non-zero median” for small factor sub-sampling (ex: 2, 3) and “non-zero mean” for large factor sub-sampling (ex: 4, 5,..). So for example when setting the sub-sampling to 4 (or 4x4), the “non-zero mean” would entail taking the average of a pixels and its 15 nearest neighbors while ignoring zeroes, and doing that on an grid subsampled by 4 in the x and y. While this will clearly affect the depth-map xy resolution, it should be noted that all stereo algorithms do involve some convolution operations, so reducing the x-y resolution after capture with modest sub-sampling (<3) will lead to fairly minimal impact to the depth x-y resolution. A factor of 2 reduction in X-Y resolution should speed subsequent application processing up by 4x, and a subsampling of 4 should decrease compute by 16x. Moreover, one benefit of the intelligent sub-sampling is it will also do some rudimentary holefilling and smoothing of the data using either a “non-zero mean” or “non-zero median” function (which has a slightly higher computational burden). The “non-zero” refers to the fact that there will be values on the depth map that are zero that should be ignored. These are “holes” in the depth map that represent depth data that did not meet the confidence metric, and instead of providing a wrong value, the camera provides a value of zero at that point. Finally, sub-sampling can actually help with the visualization of the point-cloud as well because very dense depth maps can be hard to see unless they are zoomed in.
Once the depth-map has been compressed to a smaller x-y resolution, more complex spatial-and temporal filters should be considered. We recommend first considering adding an edge-preserving spatial filter.
2. Edge-preserving filtering: This type of filter will smooth the depth noise while attempting to preserve edges. Consider the example below in Figure 1 of a 2D range data to a 10x10mm box placed near a wall, 500mm away from the depth camera. There will be noise on the depth measurement, as shown on the right. The ideal desired measurement is seen on the left. If we apply normal smoothing filters, we will see the depth noise will diminish, but we will also see the distinct edges of the box become smoothed out as well, as shown in Figure 2.
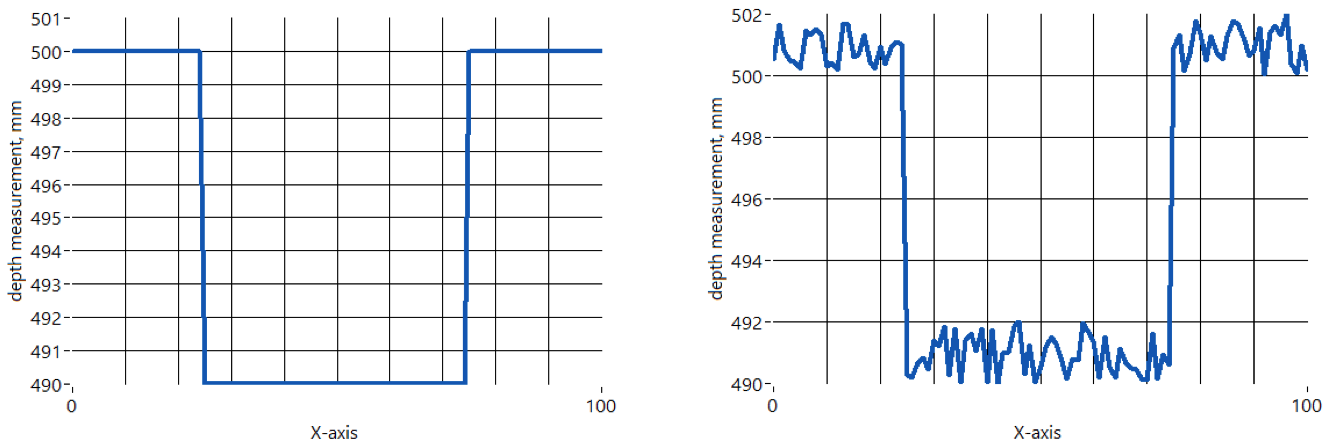
Figure 1. Conceptual cross-section of a 10x10mm box placed near a wall. A depth camera will measure the wall and the box with some depth noise, as seen on the right. The ideal noise-free measurement is seen on the left.
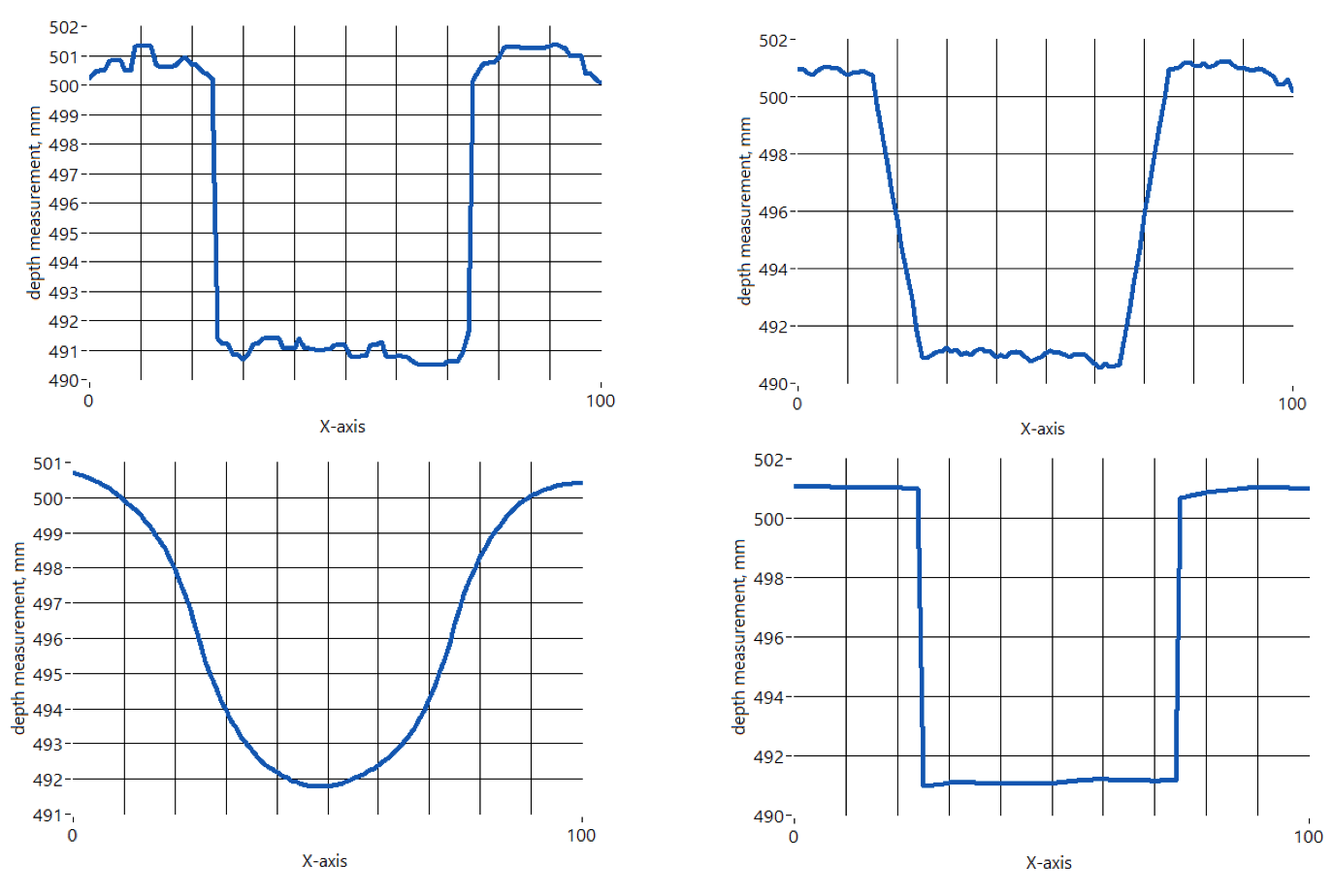
Figure 2. Applying a smoothing filter to the noisy measurement in Figure 1 will smooth the data but may result in unwanted artifacts, such as rounded or elongated edges, or overshoot. In the upper left we apply a Median Filter with left rank=5. In the upper right we apply a simple moving average of window size 13. In the lower left we apply a bidirectional exponential moving average with alpha=0.1. In the lower right, we apply the type of edge-preserving filter described in this paper, where we use an exponential moving average with alpha=0.1, but only under the condition of neighboring pixels having a depth difference of less than a threshold step-size of delta=3. This last filter will serve as the basis for the edge-preserving filter adopted here.
The edge-preserving filter we use in our `librealsense`` example is a type of simplified domain-transform filter, but we emphasize again that this is but one of many filters that can be applied. For this filter, we raster scan the depth map in X-axis and Y-axis and back again, twice, while calculating the one-dimensional exponential moving average (EMA) using an alpha(α) parameter that determines the amount of smoothing [ https://en.wikipedia.org/wiki/Moving_average ]. The specific recursive equation is:

Where the α coefficient represents the degree of weighting decrease. Yt is the newly recorded instantaneous value (of disparity or depth), and St-1 is the value of the EMA at any time period t.
Alpha=1 means no filtering, while alpha=0 means an infinite history for the filtering. However, we also add one more parameter called delta (𝛿thresh). If the depth value between neighboring pixels exceed the depth threshold set by this delta parameter, then alpha will be temporarily reset to 1 (no filtering). This basically means that if an edge is observed, then the smoothing is temporarily turned off. This will cause artifacts depending on whether the edge was traversed from the right-to-left or left-to-right, which is why we normally employ two bi-directional passes in both x- and y- which tends to be sufficient to reduce the artifacts.
However, care should be taken to use parameters that do not over-aggressively remove features. A good set of default values would be Spatial Alpha=0.6 and Spatial Delta=8, where delta is in units of 1/32 disparities, so 8 means 8/32 disparities. We do recommend adjusting these parameters for best results depending on the applications.
In our implementation we focus on a filter that uses only the depth as the input. Impressive results have also been achieved by using filters that are guided by information from the color image as well as by motion in the scene, but they are beyond the scope here.
This brings us to another aspect of spatial filtering Intel RealSense camera depth maps. For depth sensors that are based on triangulation, the nature of the measurements means that the depth noise will increase as the square of the distance away. This poses a slight challenge, because it would be necessary to make the alpha and delta parameters dependent on the range in order to get the best results, and not over-smooth near-range data, while under-smoothing far range data. Instead we recommend applying the edge-preserving filter in disparity domain (which is 1/Distance). This is why our implementation consists of a pipeline of 1. Transforming into disparity space, 2. Applying the spatial and temporal filtering, and 3. Transforming back to distance. It should be noted that the RealSense sensors can also output depth directly in disparities which would remove the need for the depth-to-disparity transform.
Another aspect of depth maps we have mentioned is the existence of “holes”. In a stereo system the holes come from either data not being available or having a too low confidence. Holes commonly result from: A. Occlusions – the left and the right images do not see the same object due to shadowing (aka occlusion). Since we reference everything to the left imager, you will see this shadowing on the left side of objects, and along the left edge of the image; B. Lack of texture – stereo matching relies on matching texture in the left and right images, so for texture-less surfaces like a flat white wall, the depth estimate can be challenging (which is why the projector is used to generate texture); C. Multiple matches – this happens when there are multiple equally good matches, such as when looking at a very uniform periodic structure; D. No signal – this happens if the images are under-exposed or over-exposed; E. Below minZ – if the object is very close, the stereo algorithm search-range is exceeded, and we have a Minimum operating distance. Objects need to be farther away than this MinZ to be seen.
Next we look at what to do when there are holes. For some applications it is best to leave the holes and do nothing. This is generally true for robotic navigation and obstacle avoidance as well as 3D scanning applications. For other applications like depth-enhanced photography, humans prefer to look at images with no holes, and a “best guess” is better than no guess.
- Spatial Hole-filling: We have a few very simple hole-filling methods in our Intel RealSense SDK API. One simple hole-filling method is to use neighboring left or right valid pixels within a specified radius to fill in the hole. This approach is implemented in
librealsenseat the spatial filtering stage for efficiency consideration.
Another simple hole-filling method (and discrete processing block) is to use left valid pixel(s) to fill in the hole since our stereo algorithm is referenced to the left imager. This is implemented in 'librealsense' library as a separate processing block, called Hole_filling_filter. Three methods for left filling are implemented in the SDK by filling the hole pixel with 1. Left valid pixel value, 2. The biggest (farthest away) among the valid five upper left and down pixel values (used for depth map), and 3. The smallest among the valid five upper left and down pixel values (used for disparity map). All these conditions favor assuming that a hole should be filled with the nearest background image, as opposed to foreground value of a scene, and works well for occlusion filling.

Figure 3. Applying a hole-filling using the discrete hole filling processing block has three options for filling.
Returning now to improving the depth noise in post-processing, we note that another very important noise contribution is the temporal noise. The Intel RealSense D4xx sensors do not have any knowledge of priors or history, so each depth frame is calculated completely independently of a previous frame and is completely deterministic. However, there is noise on the input images that can stem from inherent sensor noise, environmental noise (lighting changes), or motion, or projector noise. All these sources contribute to some depth noise in time. In general this means that data quality can be improved by either running at lower frame rates and integrating the exposure longer, or, as will be discussed next, by applying some temporal averaging to each pixel in the depth-map.
- Temporal filtering & persistence: Whenever possible, it is recommend to use some amount of time averaging to improve the depth, making sure not to let “holes” (depth=0) influence the calculations. In the 'librealsense' implementation we stick with the same type of exponential moving average (EMA) filter that we used for spatial filtering. Like before, there will be an alpha parameter which will represent the extent of the temporal history that should be averaged. The benefit of this approach is that “fractional” frames can essentially be averaged. By setting alpha=1, there will be zero filtering, but reducing alpha to near 0, will increase averaging and smoothly. So it is not a simple discrete “average 2 or 3 or 4 frames”, but allows for much more fine grained smoothing. Moreover, just like with the spatial averaging, it is important to add a threshold parameter, delta. This way we try to reduce temporal smoothing near edges, and we also do not include holes (z=0) in the averaging. Some good default values for the temporal filter are alpha=0.5 and delta=20.
Another temporal filter we offer as on option, is the “persistence filter”. This is essentially a filter that can be used to see farther. For every depth pixel, the filter will look at the history of holes, and will retain the last valid value seen, within a specified number of frames, from 0-7. A persistence value of 8 means that we will retain the last valid value indefinitely, while a value of 1 means only look one frame back in history if you see a hole, otherwise use the latest value (i.e. the z=0). So when pointing the camera in the dark into a large room, at a certain range the valid depth values will start to give way to holes. If you use the persistence feature, you will see much farther because it will persist pixels. In other words, this is a type of hole-filling algorithm, but it bases its guess on having seen a good value there in the past, as opposed filling based on neighboring pixels. Of course, all hole-filling algorithms are prone to some errors and artifacts and should be used after careful consideration of the tradeoffs. In the specific case of this persistence filter, there will be an artifact where if you wave an object in front of the camera, you will see a different in-filling behavior depending on whether you move the object left or right on the scene. A movement right will persist values from the object into the occlusion region, making the object wider, whereas a movement left will persist values from the background (which is better). As with all algorithms this can be fixed with more levels of logic, but is beyond current scope and implementation.
Implementing Post-Processing with Intel RealSense SDK API
In the librealsense API, post-processing is handled as a sequence of “processing-blocks”. The concept is fairly simple and is shown in Figure 4. See example of post-processing.
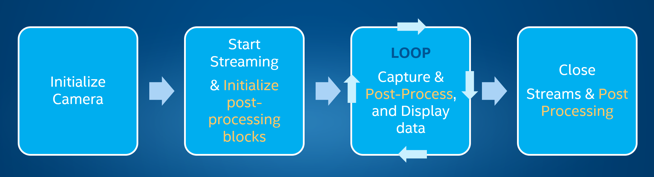
Figure 4. This shows the normal flow for working with a RealSense™ camera by initializing, starting streaming, looping capture of data, and finally closing all streams. In orange is shown the additional steps needed when adding post-processing.
First, the post-processing “Block” and queues need to be initialized for ALL the processing steps before capturing is started. This is done by using the following set of three commands, for each processing block:
Initialization sequence:
rs2_frame_queue* rs2_create_frame_queue(int capacity=1, rs2_error** error);
rs2_processing_block* rs2_create_XXX_filter_block(rs2_error** error);
void rs2_start_processing_queue(rs2_processing_block* block, rs2_frame_queue* queue, rs2_error** error);
Note that the XXX denotes the different filters:
rs2_processing_block* rs2_create_spatial_filter_block(rs2_error** error);
rs2_processing_block* rs2_create_decimation_filter_block(rs2_error** error);
rs2_processing_block* rs2_create_disparity_transform_block(unsigned char transform_to_disparity, rs2_error** error);
rs2_processing_block* rs2_create_temporal_filter_block(rs2_error** error);
rs2_processing_block* rs2_create_hole_filling_filter_block(rs2_error** error);
The disparity transform block has a “transform_to_disparity” flag which indicates whether it is a transform from depth-to-disparity (=1) or from disparity-to-depth (=0). A processing block should be initialized for each of these separately.
After initializing, it is necessary to set the processing filter parameters. This can be done at any time during streaming.
Setting Processing Filter Parameters:
The filter parameters can be set using the SetOption command:
void rs2_set_option(const rs2_sensor* sensor, rs2_option option, float value, rs2_error** error);
There are 4 of the enumerated options that are relevant:
36 - RS2_OPTION_FILTER_MAGNITUDE
37 - RS2_OPTION_FILTER_SMOOTH_ALPHA
38 - RS2_OPTION_FILTER_SMOOTH_DELTA
39 - RS2_OPTION_HOLES_FILL
It is important to note that for the “sensor” pointer in set_option, it should instead be the pointer to the specific “Processing Block”. So for example, if we want to set the ALPHA parameter for the temporal filter, we would use the pointer to the temporal filter block.
For the decimation block the only option needed is:
Filter magnitude = sub-sampling number (ex: 2, 3, 4..)
For the spatial filter block there are four options:
Filter magnitude = iterations of the filter. We recommend using 2 (default).
Filter smooth alpha = the spatial alpha parameters (0-1)
Filter smooth delta = the spatial delta threshold in 1/32 disparities. Default is 20, but try 8 as well.
Filter holes fill = the spatial radius for hole filling (0=none, 1=2 pixels, 2=4 pixels, 3=8 pixels, 4=16 pixels, 5=unlimited).
For the temporal filter block the 3 options are:
Filter smooth alpha = the temporal alpha parameters (0-1)
Filter smooth delta = the temporal delta threshold in 1/32 disparities. Default is 20.
Filter holes fill = the persistence value (0=no persistence, and 8=persist indefinitely)
For the separate hole-filling block there is only one option:
Filter holes fill = additional filling of holes based on choosing nearest neighbor filled with 0=Use left pixel to fill, 1=Max of nearest pixels on left, and 2=Min value of nearest pixels on left, as shown in Figure 3.
Once all the filters have been initialized, we have nice flexibility in how we process a frame during streaming. The normal flow of capturing data in a loop is to use the wait_for_frame command.
rs2_frame* rs2_wait_for_frame(rs2_frame_queue* queue, unsigned int timeout_ms, rs2_error** error);
This is a blocking call. As soon as a new frame arrives, this frame can be analyzed and the data can be dispositioned and displayed, before the frame is released, and the process is repeated.
However now we can add post processing to the flow in whatever order we want. The recommend flow is shown in Figure 5.

Figure 5. In the capture loop, the processing flow can be defined freely by using the “process frame” command, and passing the frame pointers, before releasing at the end.
The command for applying filtering is to take the latest frame as input and to execute the desired processing command multiple times in sequence:
void rs2_process_frame(rs2_processing_block* block, rs2_frame* frame, rs2_error** error);
Where the processing block pointer specifies the specific post-processing step. The output frame from each step will then be the input frame to the next processing block, and so on. Only the final processed frame needs to be released before repeating the loop.
Example Results and trade-offs
We now turn to exploring a few examples, the effects of the settings, as well as the computational burden.
First we address the question of the computational burden. Figure 6 shows a breakdown of the time it takes to complete each step, in milliseconds, and on Intel i7 laptop. We benchmark here only for one PC in order to show the relative processing times of the filters. Clearly these times will be dependent on the specific compute platform being used.
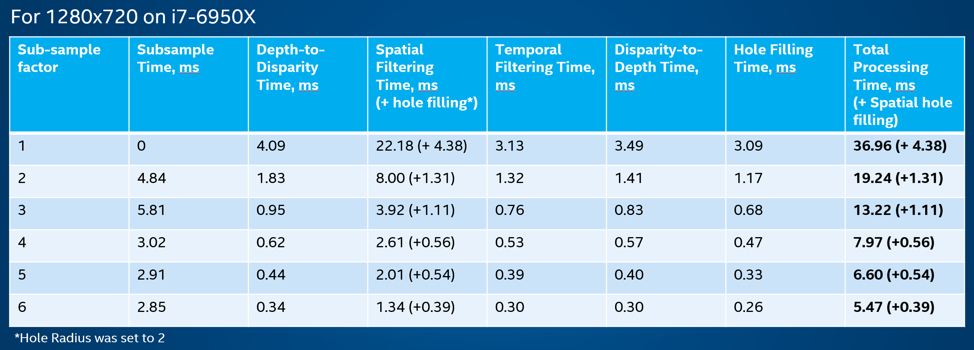
Figure 6. This details the time it takes to perform post-processing on a two different PC platforms. This is meant primarily to give some insight into where the main processing burden is. These are all done assuming single threaded implementation on the CPU.
By adjusting the subsampling number from 1 (no-subsampling) to 6, we see that total processing time is reduced from 37ms to 5.5ms. We also see that the spatial filter is the most time-consuming for low subsample (high output resolution), but for high subsample (low output resolution) the spatial filtering time is reduced from 22ms to 1.34ms. It should also be noted that these filters have not been optimized by any use of special instruction or parallel processing, so as to keep the code portability as high as possible. For many applications the best trade-off is likely to be a sub-sampling of 3 when starting with 1280x720 resolution which, without the use of hole-filling, takes 12.5ms for all post-processing.
The temporal filter is seen to be quite efficient, and uses only a single full frame of memory. At a sub-sample factor of 3 (taking 5.8ms), the temporal filter takes only 0.76ms, irrespective of the filter alpha or delta parameter choice.
Turning now to the effect of the filters, we will show some qualitative results for a specific single scene. The test scene is shown in Figure 7. It is a white Intel RealSense packaging box, and a black leather notebook on a flat textured surface.

Figure 7. Test scene as seen through the left stereo imager on an Intel RealSense D415 depth camera. This is a Intel RealSense packaging box and a black shiny leather notebook in front of a textured background. Resolution 1280x720. (Note: This is not using the 3rd color camera in the system).
In Figure 8, we see the same scene with color and depth map, when the laser projector is turned on at low power. The color image on the left now shows the projector pattern on the box.
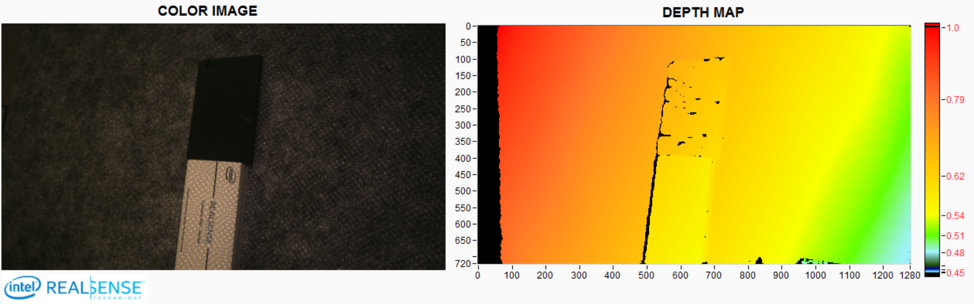
Figure 8. Same scene as Fig 7, with IR projector turned on, and showing depth map on the right. The plane is slightly tilted, but the nominal range to the box is 58cm. The “High Density” Depth preset is used. We decreased the laser projector so we see some holes on the black notebook (with default laser power, no holes are visible). We notice that there are holes on the left side of the box due to occlusions.
If we turn on the “persistence” filter we see that the holes on the notebook mostly disappear, as shown in Figure 9.
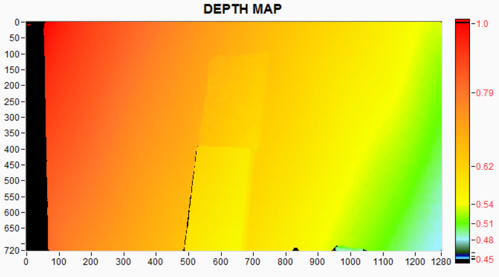
Figure 9. The same scene with the persistence filter set to 8, showing how we improve the depth image and fill holes.
If we instead turn on the spatial filter hole-filling block we see that the holes near the box and notebook disappear and are replaced by background. While this in-filling appears to work well in the middle of the notebook and for the occlusions near the Intel RealSense box, near the edges of the notebook we see that the holes have been replaced with the depth from the background leaving the impression of a badly torn notebook. For many applications it may be better to leave a hole, than to give false values.
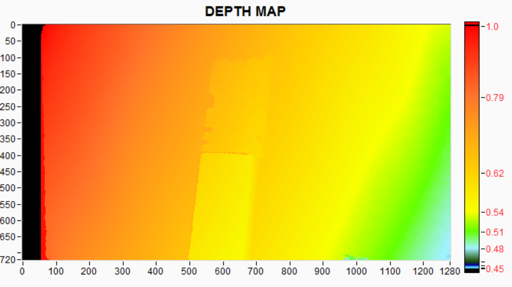
Figure 10. Using simple “Hole fill” (left in-fill), also removes all holes, but tends to add some artifacts, like the book having background holes.
For the rest of this paper we will focus on the point-cloud visualization, which is the best approach to viewing spatial noise, especially if we do not apply color image texture to the mesh which can tend to hide data. As a starting reference point, we measure the background tilted plane-fit RMS noise on a small patch near the right of the box. The RMS noise is about 0.6mm, or 0.085 subpixel RMS noise, with the projector off. With the projector turned on at 70mW (lower than default of 150mW), this actually degrades to 0.7mm or 0.1 sub-pixel RMS noise (see our other tuning paper for why this is the case).
Figure 11 shows the simple un-textured point cloud for subsampling of 1 (none), 2, 3. ]



Figure 11. This shows the point-cloud of the scene for subsampling=1, 2, 3.

Figure 12. Effect of time averaging. Left is raw image, and right uses a temporal filter.
To examine the effect of time averaging it is most pronounced when seeing it live or on a video, which we cannot do in this paper. Instead, Figure 12 tries to show a case of aggressive temporal filtering (alpha=0.1, and delta=20) with the projector on. The improvement of the depth noise is most pronounced on the black notebook where the RMS noise goes from 2mm (0.32 subpixel) to 1.1mm (0.15 subpixel). For the background with projector turned off, the same temporal filter improves RMS from 0.40mm (subpixel=0.07) to 0.29mm (subpixel=0.05). We should note that when doing measurements at near range where the RealSense depth cameras can provide better than 1mm depth resolution, it is best to set the “depth units” (the depth step size) to 100um instead of the default 1000um or you will see quantization steps in the depth, as described in the Tuning white paper. If you do this, then the delta parameters should be scaled by 10 as well.
Turning the temporal filtering off and now turning the spatial filter on, we see in Figure 13 that we can smooth the spatial depth noise. In this example we set the spatial alpha=0.4, with delta=100 (upper right image) and delta=4 (lower right image), respectively. This clearly shows the edge-preserving nature of the spatial filter. With delta=100, the step size between neighboring pixels never exceeds 100/32=3.12 disparities for this scene, so the edges of the boxes are smoothed, i.e the edges are not preserved. For delta=4, we recover the edges while still smoothing the flat surfaces.
Finally, in the lower right of Figure 13, we show the scene with all filtering turned on – spatial, temporal, and persistence, showing the improvement over the raw scene in the upper left.

Figure 13. Effect of spatial filtering. The upper right is the raw depth map. The upper right is a smoothed depth map without any edge preserving. The lower left is the same smoothed depth-map but with spatial delta=4, and finally in the lower right we combine the temporal and spatial filters.
Conclusion
We have shown here a set of post-processing filters that can be applied to the depth map of the Intel RealSense cameras to improve the depth. This is meant to show just one example of a way to “clean up” depth images, well knowing that there are always going to be trade-offs in compute or introduction of some artifacts. For example, temporal filtering can help reduce the depth noise >2x, but should be used sparingly on scenes with high-speed motion. For spatial filtering, we demonstrated an edge-preserving filter that can smooth an image while attempting to preserve true features. We also demonstrated the use of a persistence filter that can be used to increase the range of a system, in particularly in the dark. All these filters are open sourced and available in the Intel RealSense SDK 2.0 and have been architected to be easy to apply in different sequences.
Updated about 5 years ago
